轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
轴承有限元分析怎么做？
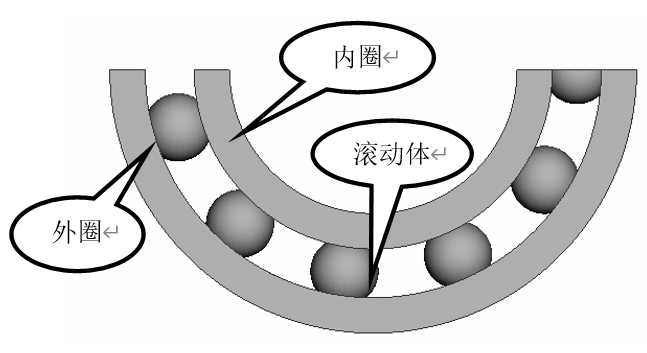
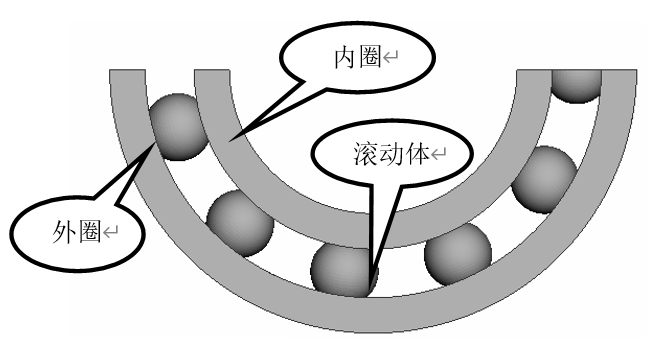
滚动轴承是机械传动中非常重要的部件，它依靠滚动体与内、外圈的滚动接触把转动部件支撑起来，实现力和运动的传递，其结构性能的好坏直接关系到整个机械系统的可靠性。
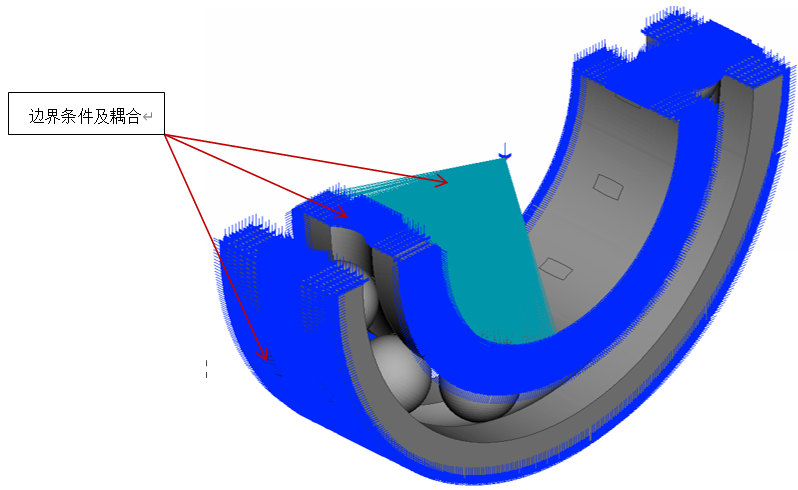
滚动轴承如图1‑1所示，该系统包含滚动体-滚珠、内圈、外圈三个部分。
计算要求
滚动轴承的接触在载荷为零时为点接触，受载后接触区域扩展为一个斑，一个椭圆接触面。本项目旨在进行滚动轴承在径向载荷条件下滚动体与内外圈接触处的接触应力的分析计算。
几何简化以及网格划分
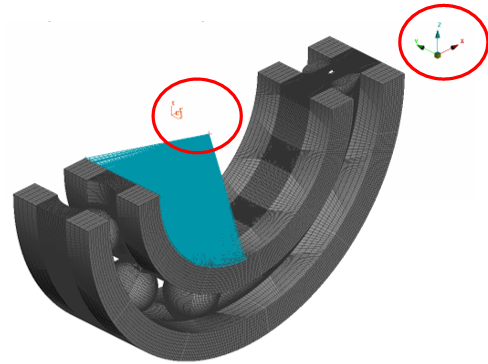
模型的网格全部采用六面体实体网格，如图2‑1所示为滚珠中面上的网格分布。为了更准确地模拟接触区域的接触情况，在预估的接触区域划分的单元尺寸为0.05mm的规则均匀网格。滚动轴承网格模型中实体网格单元共有1639061个。
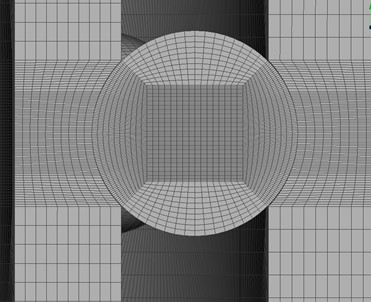
六面体网格部件
全模型网格
模型的分析步及边界条件
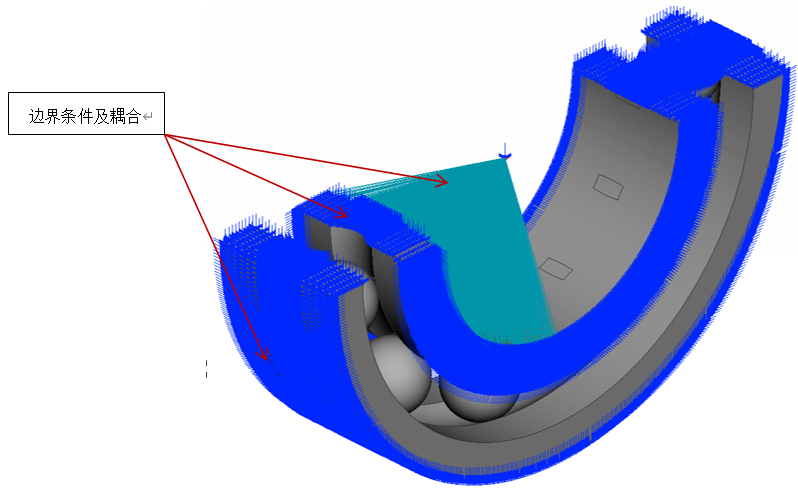
工况的设定及求解
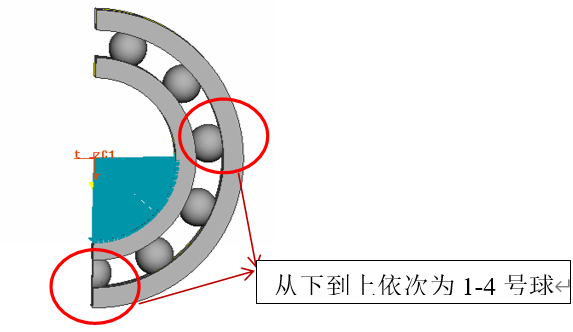
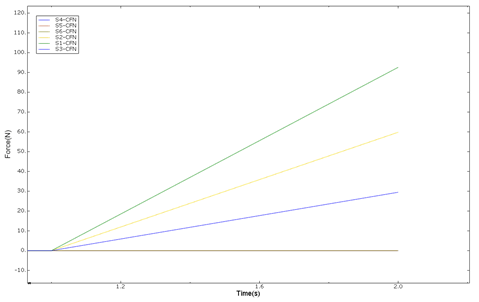
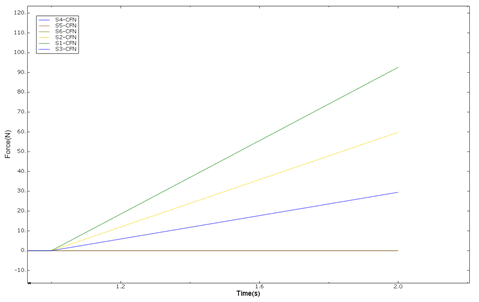
工况1的接触力输出图
|
工况1 |
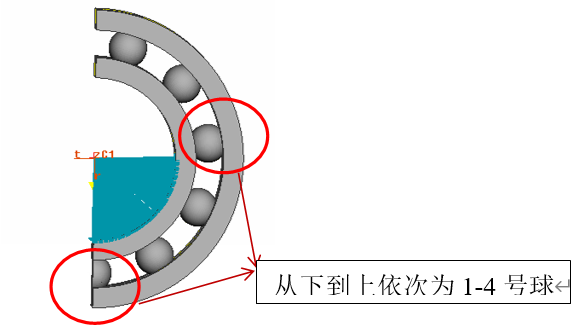
1号球 |
2号球 |
3号球 |
4-6 |
工况2 |
1号球 |
2号球 |
3号球 |
4-6 |
|
|
92.5995 |
59.8032 |
29.4905 |
- |
|
112.421 |
63.2666 |
4.21357 |
- |
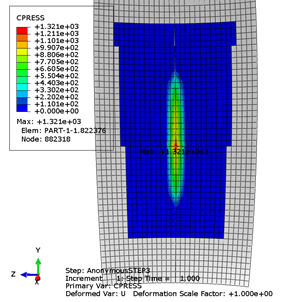
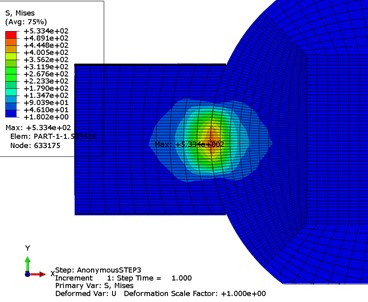
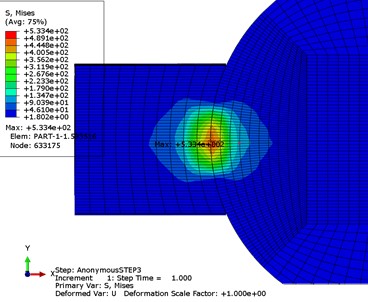
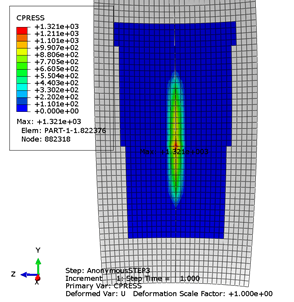
1号球内圈接触区域云图
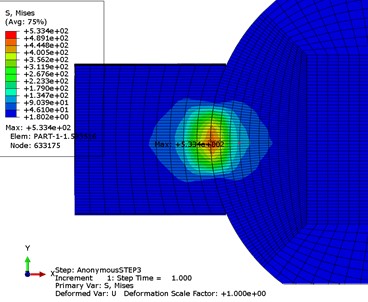
1号球与内圈接触区域的等效应力分布（接触应力最大处）
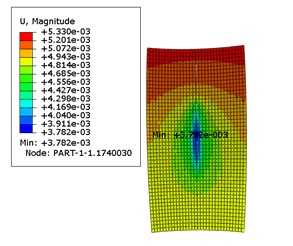
1号球与内圈接触区域的位移分布（接触应力最大处）
应用赫兹理论求解
赫兹弹性接触理论可以用来估算滚动轴承的接触应力和变形。参考冈本纯三的《球轴承的设计计算》中的计算方法。这里仅计算接触应力最大的球与内圈的接触情况。轴承的材料参数采用仿真参数设计，内外圈与钢球的参数一致，形状参数如表4-1所示：
|
球的两凸面半径/mm |
内圈的凹面半径/mm |
内圈的凸面半径/mm |
钢球数/个 |
径向载荷/N |
|
3.572 |
3.67 |
17.678033 |
11 |
300 |
有限元解与赫兹理论解的误差
|
|
受力参数 |
Hertz理论解 |
有限元解 |
误差 |
|
工况一 1号钢球与内圈接触 |
最大接触应力 |
1267.72 |
1321 |
0.04% |
|
最大接触变形 |
0.00283 |
0.00368 |
23.1% |
|
|
接触椭圆长轴 |
0.846 |
0.898 |
8.42% |
|
|
接触椭圆短轴 |
0.124 |
0.14 |
11.4% |
